Home | Research & Projects | Photographs & Drawings | Other

SBI and the Dodelson-Schneider effect

SBI has it's own Dodelson-Schneider effect (but it knows that it does)

Jed Homer, Oliver Friedrich & Daniel Gruen [2412.02311]

Can generative models really be used for inference? What are they really doing?

The bad news is that, contrary to commonly held beliefs, SBI methods cannot escape (nor should they!) the effects of covariance estimation - the models cannot invent information upon the likelihood from simulations.

The good news is that generative models, when used for simulation-based inference (SBI; as a density estimator for either the likelihood or the posterior), can reliably fit the target distribution and be used in Bayesian inference problems.

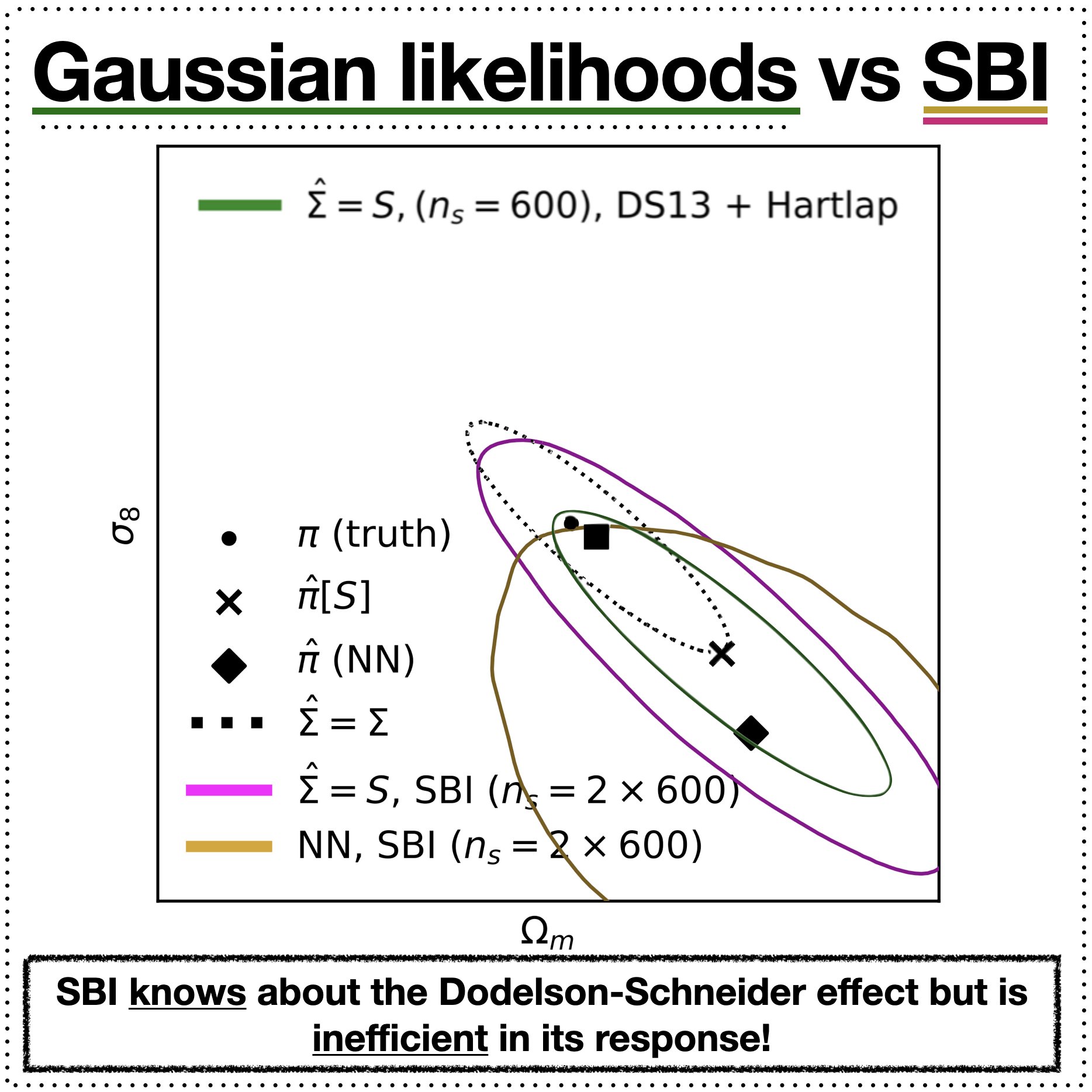
Work done with Oliver Friedrich (USM/LMU) and Daniel Gruen (USM/LMU).

SBI and the one-point matter PDF

A Point Unknown: Unlocking information in the one-point matter PDF.

Jed Homer, Oliver Friedrich Cora Uhlemann & Daniel Gruen [in prep.]

SBI is necessary for when we do not know the likelihood function; the function that tells us the probability of our data given a parameterisation of our model. When the form is non-Gaussian, it is difficult to model analytically and verify in an analysis.

The question is, can SBI methods reliably extract more information when we know they should?

The one-point matter PDF is a counts-in-cells statistic that is sensitive to the higher-order moments of the density field - it can extract information beyond the 2pt function for non-Gaussian fields. However, as alluded to on this page, this information is shrouded in our uncertainty upon the form of the likelihood function!

Baryonification with generative models

Work in progress with Dr. Jozef Bucko and Dr. Tomacz Kacprzak at ETH Zürich.

Note: This .gif is a bit slow.

Generative models

Generally speaking, the likelihood is not known in an inference problem. Speaking more generally still, this limits the amount of information we can extract from our data upon fundamental physical parameters.

Generative models posit (very tenuously!) an interesting solution to this problem by parameterising the likelihood with a set of parameters (usually of order millions to billions of them) and an architecture - all fit by maximum likelihood (or score-matching etc.).

I'm interested in the limitations of this paradigm (e.g. simulation-based inference, density deconvolution).

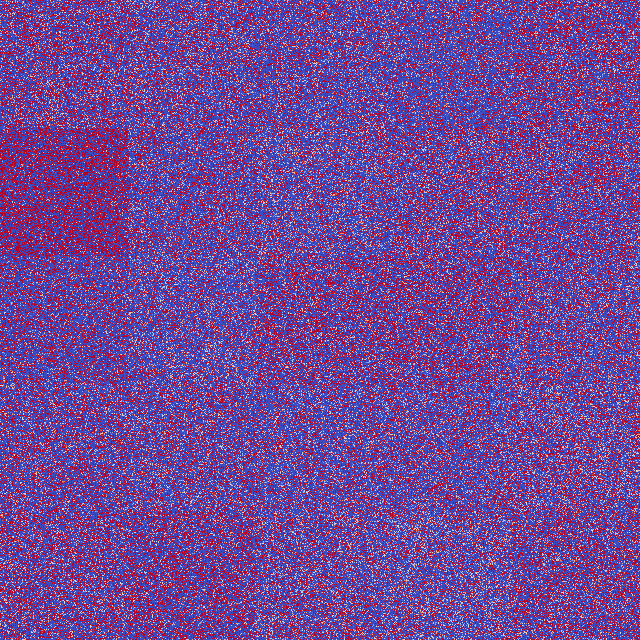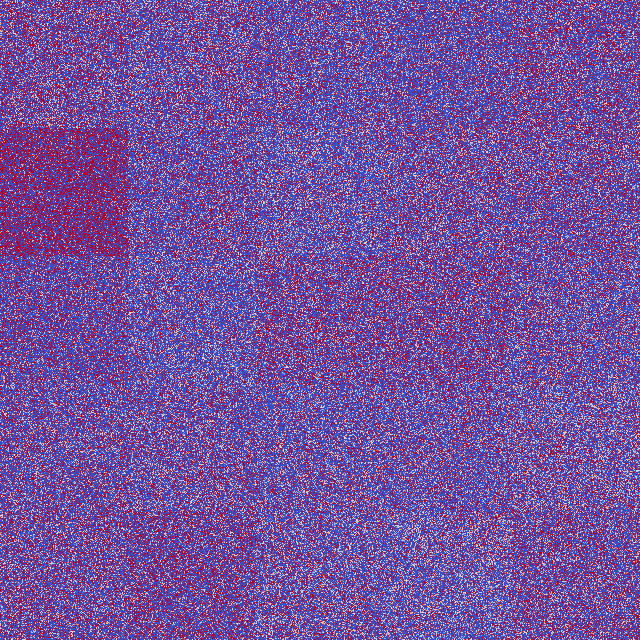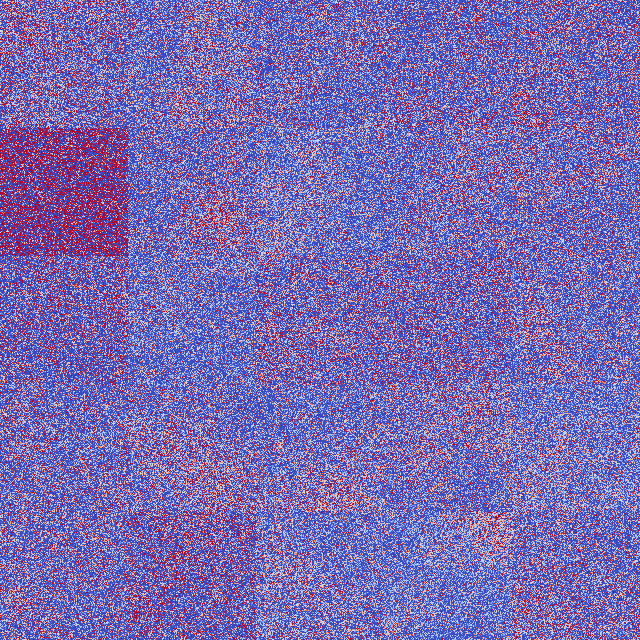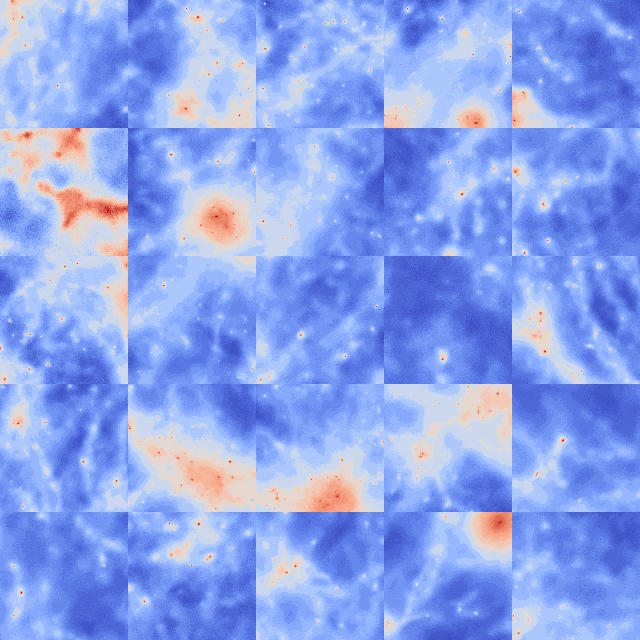
`JIFTY` + `SBGM`

This plot shows signal reconstructions (middle row) from noisy data (top row) using a diffusion model prior.

The posterior samples (bottom row) are drawn using Metric Gaussian Variational Inference from Knollmüller and Enßlin (2019).

MGVI is implemented in the NIFTY probablistic programming package, it is built from jax.

This is fitting a many million dimensional posterior to the latent variables of the generative model.

It works quite nicely (these samples are from the first iteration only!), I plan to extend this to parameter inference problems.

Interpretable SBI

What is a generative model really doing?
How does a model deviate from a simple linear function of the parameters?
Is the noise in the data Gaussian or not?
Is this method actually interpretable?

These are central questions posed for analyses that use simulation-based inference methods. The likelihood estimators do not produce a symbolic description and it is hard to know if you can trust an analysis using these tools. This isn't news - but what if a model could quantify deviations from a simple analytic model?

This question involes the functional form of the likelihood of the data given the model as well as the functional form of the data expectation given the model parameters. You'd like to be able to interpret these separately, understanding what a generative model does to describe the expectation when it is fit to simulations that you don't have an analytic likelihood for.

I think you can do this via expectation-maximisation of a conditional generative model. First, you model your expectation, then you maximise its log-probability conditioned on the data.

`sbgm`

A code for fitting score-based diffusion models in jax.

See here.

pip install sbgm

`sbiax`

This is a code for implementing your own SBI experiments and analyses.